Answer:
x=0.4771
Explanation:
Given the equation:
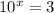
Whenever the unknown is in the exponent, it is best to take the logarithm of both sides of the equation.
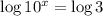
Next, apply the power law of logarithms to the left-hand side of the equation above:
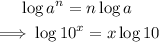
Thus, the last result can be written in the form below:
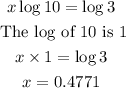
The value of x is approximately 0.4771.