Given in the question:
a.) The first costs $5 upfront and $4 per kilometer.
b.) The second costs $15 plus $3 per kilometer.
Let's generate the equation of each of the car service charges,
Let,
y = total cost of service
x = distance traveled
a.) The first costs $5 upfront and $4 per kilometer.
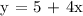
b.) The second costs $15 plus $3 per kilometer.
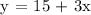
Let's determine the driving distance when the two companies charge the same.
We get,
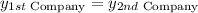

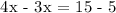
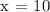
Therefore, the two companies charge the same at a driving distance of 10 kilometers.
Summary:
1. The system of equations.
y = 5 + 4x
y = 15 + 3x
2. The solution.
x = 10
3. Graphing the system of equations.