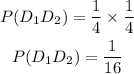Solution:
Given:
A 52-card deck
There are four suits in a standard deck of cards, Clubs, Hearts, Spades, and Diamonds.
There are 13 diamond cards.
Hence,

Probability is calculated by;
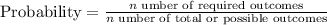
Thus, the probability of drawing a diamond on the first draw is;

Since two draws are made with replacement, the cards are completed back again before the next draw.
Hence, the probability of drawing a diamond on the second draw is;

Therefore, the probability of drawing a diamond each time;