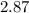Question

1 Type the correct answer in each box. Use numerals instead of words, Consider this quadratic equation, x2 + 2x + 7 = 21 The number of positive solutions to this equation is The approximate value of the greatest solution to the equation, rounded to Reset

Answer 1

The number of positive solutions to this equation is;

`1`

The approximate value of the greatest solution to the equation is;

`2.87`

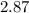
Step-by-step explanation:

Given the equation;

`x^2+2x+7=21`

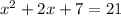
Let us subtract 21 from both sides;

`\begin{gathered} x^2+2x+7-21=21-21 \\ x^2+2x-14=0 \end{gathered}`

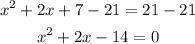
We can now solve for x using the quadratic formula;

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

from the equation;

`\begin{gathered} a=1 \\ b=2 \\ c=-14 \end{gathered}`

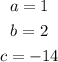
substituting;

`\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4(1)(-14)}}{2(1)} \\ x=\frac{-2\pm\sqrt[]{4+56}}{2} \\ x=\frac{-2\pm\sqrt[]{60}}{2} \end{gathered}`

so, we have;

`\begin{gathered} x=\frac{-2\pm\sqrt[]{60}}{2} \\ x=\frac{-2+\sqrt[]{60}}{2} \\ x=2.87 \\ \text{and} \\ x=\frac{-2-\sqrt[]{60}}{2} \\ x=-4.87 \end{gathered}`

Therefore, the number of positive solutions to this equation is;

`1`

The approximate value of the greatest solution to the equation is;

`2.87`