We have the following quadratic function:
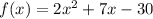
And we need to find its zeros i.e. the solutions to the equation:
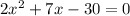
Given a quadratic equation like the following:
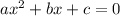
Its solutions are given by the quadratic solving formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In our case we have a=2, b=7 and c=-30. Then we get:
![x=\frac{-7\pm\sqrt[]{7^2-4\cdot2\cdot(-30)}}{2\cdot2}=\frac{-7\pm\sqrt[]{49+240}}{4}=\frac{-7\pm\sqrt[]{289}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/sbt7y7ntknyqw4e8hme3dmexf9smogntoh.png)
So we continue:
![x=\frac{-7\pm\sqrt[]{289}}{4}=(-7\pm17)/(4)](https://img.qammunity.org/2023/formulas/mathematics/college/jaoa9388xowua8bphlcr3o28bxs79lx8mw.png)
So we have two solutions:
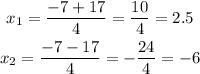
Then the answers are -6 and 2.5.