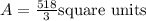Question

Find the area between the graph of ….and the r-axis on the interval [9, 16]. Write the exact answer. Do not round.

Answer 1

The area under a curve between two points can be found by doing a definite integral between the two points.

To find the area between the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.

Given the function;

`f(x)=7\sqrt[]{x}`

and the x-interval is;

`\lbrack9,16\rbrack`

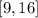
Thus, the area A between the graph and the x-interval is;

`A=\int ^(16)_97\sqrt[]{x}dx`

Next, we evaluate the integral, we have;

`\begin{gathered} \int 7\sqrt[]{x}dx=\int 7x^{(1)/(2)}dx \\ \int 7\sqrt[]{x}dx=\frac{7x^{(1)/(2)+1}}{(1)/(2)+1} \\ \int 7\sqrt[]{x}dx=\frac{7x^{(3)/(2)}}{(3)/(2)} \\ \int 7\sqrt[]{x}dx=\frac{14x^{(3)/(2)}}{3}+c \\ \text{Where c is the integral constant} \end{gathered}`

Then, we should apply the integral limits, we have;

`\begin{gathered} \int ^(16)_97\sqrt[]{x}dx=\lbrack\frac{14x^{(3)/(2)}}{3}\rbrack^(16)_9 \\ \int ^(16)_97\sqrt[]{x}dx=((14)/(3)(16)^{(3)/(2)})-((14)/(3)(9)^{(3)/(2)}) \\ \int ^(16)_97\sqrt[]{x}dx=(14)/(3)(64-27) \\ \int ^(16)_97\sqrt[]{x}dx=(14)/(3)(37) \\ \int ^(16)_97\sqrt[]{x}dx=(518)/(3) \end{gathered}`

Thus, the area A between the graph and the x-interval is;

`A=(518)/(3)\text{square units}`