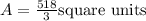The area under a curve between two points can be found by doing a definite integral between the two points.
To find the area between the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.
Given the function;
![f(x)=7\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/yubfnzo012snkgk0ganef07ajtexdkddq3.png)
and the x-interval is;
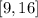
Thus, the area A between the graph and the x-interval is;
![A=\int ^(16)_97\sqrt[]{x}dx](https://img.qammunity.org/2023/formulas/mathematics/college/uugqoqieyi1tlrk7o1siml6znv12pe23a0.png)
Next, we evaluate the integral, we have;
![\begin{gathered} \int 7\sqrt[]{x}dx=\int 7x^{(1)/(2)}dx \\ \int 7\sqrt[]{x}dx=\frac{7x^{(1)/(2)+1}}{(1)/(2)+1} \\ \int 7\sqrt[]{x}dx=\frac{7x^{(3)/(2)}}{(3)/(2)} \\ \int 7\sqrt[]{x}dx=\frac{14x^{(3)/(2)}}{3}+c \\ \text{Where c is the integral constant} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pzk7r18h5rijf3ys1h1th6w5si459bs1pf.png)
Then, we should apply the integral limits, we have;
![\begin{gathered} \int ^(16)_97\sqrt[]{x}dx=\lbrack\frac{14x^{(3)/(2)}}{3}\rbrack^(16)_9 \\ \int ^(16)_97\sqrt[]{x}dx=((14)/(3)(16)^{(3)/(2)})-((14)/(3)(9)^{(3)/(2)}) \\ \int ^(16)_97\sqrt[]{x}dx=(14)/(3)(64-27) \\ \int ^(16)_97\sqrt[]{x}dx=(14)/(3)(37) \\ \int ^(16)_97\sqrt[]{x}dx=(518)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nbcv2c9pegsz1j2sqr3wyd3xg7toy8zd5i.png)
Thus, the area A between the graph and the x-interval is;