Question

A 3.31-g sample of lead nitrate, Pb(NO3)2, molar mass = 331 g/mol, is heated in an evacuated cylinder with a volume of 1.62 L. The salt decomposes when heated, according to the equation2Pb(NO3)2(s) 2PbO(s) + 4NO2(g) + O2(g)Assuming complete decomposition, what is the pressure in the cylinder after decomposition and cooling to a temperature of 300 K? Assume the PbO(s) takes up negligible volume.a)0.380 atmb)0.228 atmc)0.0342 atmd)1.38 atme)none of these

Answer 1

2Pb(NO3)2(s) => 2PbO(s) + 4NO2(g) + O2(g)

We have this reaction in a cylinder and also have 300 K. We are going to make some assumptions about these gases inside the cylinder: gases are ideal.

Then we will use this formula:

`p\text{ x V = n x R x T}`

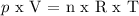
p = pressure in the cylinder

V = volume

n = moles

R = gas constant

T = temperature

Procedure:

1) We must calculate first how many moles we have after the decomposition of Pb(NO3)2, I mean how many moles of NO2(g) and O2(g) we have.

Note: PbO (s) takes up negligible volume (read the text please)

Let's calculate how many moles of Pb(NO3)2 is heated:

Moles Pb(NO3)2 = mass / molecular weight = 3.31 g / 331 g/mol = 0.01 moles

Using the reaction and stoichiometry we will calculate moles for NO2 and O2:

For NO2) 2Pb(NO3)2(s) => 2PbO(s) + 4NO2(g) + O2(g)

2 moles Pb(NO3)2 --------- 4 moles NO2

0.01 moles Pb(NO3)2---------- x = 0.02 moles NO2

For O2) 2Pb(NO3)2(s) => 2PbO(s) + 4NO2(g) + O2(g)

2 moles Pb(NO3)2----------- 1 mol O2

0.01 Pb(NO3)2 ------------ y = 0.005 moles O2

------------------------------------------------------------------------------------------------------

2) Inside the cylinder we have:

Total moles = moles NO2 + moles O2 = 0.02 + 0.005 = 0.025 moles

--------------------------------------------------------------------------------------------------------

3) Using Ideal gas law and clearing the pressure:

V = 1.62 L

n = 0.025 moles

T = 300 K

R = 0.0820 atm x L / mol x K

`\begin{gathered} p\text{ = }\frac{0.025\text{ moles x 0.082 }\frac{atm\text{ x L}}{\text{mol x K}}\text{ x 300 K}}{1.62\text{ L}}= \\ =0.3796\text{ atm = 0.380 atm (3 significant digits)} \end{gathered}`

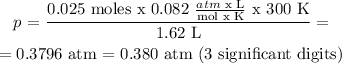
Answer: a) 0.380 atm