To reflect one point about a horizontal line, we want the image and the preimage to be equidistant to that line.
Then, to reflect for example point (8,8) about the line y = -1, we need to find a point with the same x-coordinate and whose distance to line y = -1 is the same.
The distance from point 8,8 to line y = -1 is 8 - (-1) = 8 + 1 = 9.
Then, a point that is 9 units down the line y = -1 will be (8,-10) since -1 - (-10) = -1 + 10 = 9.
We found then that to reflect about a line y = a, we need to add twice a to the negative y coordinate:
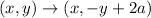
Then, for reflection about y = -1:
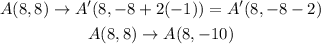
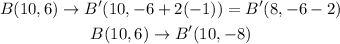
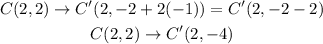
Now we need to use the same equation:
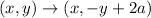
To transform the new images, which are:
A'(8,-10)
B'(10,-8)
C'(2,-4)
Applying the same for them:
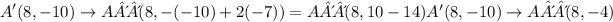
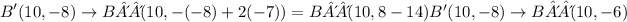
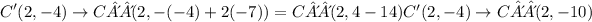
Now we have all the blanks:
For the reflection about y = -1:
A'(8, -10)
B'(10, -8)
C'(2, -4)
For the reflection about y = -7:
A'(8, -4)
B'(10, -6)
C'(2, -10)