Question

Estimate the area under the curve. Answer to the nearest integer.

Answer 1

The diagram below represents the area approximated using rectangular elements,

The interval width when an interval [a,b] is divided into 'n' rectangles is given by,

`\Delta x=(b-a)/(n)`

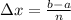
According to the given problem,

`\begin{gathered} f(x)=x^2+3x \\ a=1 \\ b=5 \\ n=4 \end{gathered}`

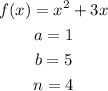
Then the width of each interval will be,

`\begin{gathered} \Delta x=(5-1)/(4) \\ \Delta x=(4)/(4) \\ \Delta x=1 \end{gathered}`

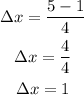
The left end-points of the approximating rectangles are,

`1,2,3,4`

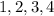
The value of the function at that left end-point gives the height of that rectangle. So the height of each rectangle will be,

`\begin{gathered} f(1)=(1)^2+3(1)=1+3=4 \\ f(2)=(2)^2+3(2)=4+6=10 \\ f(3)=(3)^2+3(3)=9+9=18 \\ f(4)=(4)^2+3(4)=16+12=28 \end{gathered}`

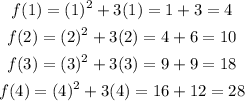
Then the approximate area (A) under the curve between the limits is given by the sum of the areas of all these 4 approximating rectangles,

`\begin{gathered} A=\mleft\lbrace\Delta x\cdot f(1)\}+\mright?\lbrace\Delta x\cdot f(2)\}+\lbrace\Delta x\cdot f(3)\}+\lbrace\Delta x\cdot f(4)\} \\ A=\Delta x\cdot\mleft\lbrace f(1)+f(2)+f(3)+f(4)\}\mright? \end{gathered}`

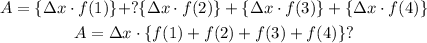
Substitute the values and simplify,

`\begin{gathered} A=1\cdot(4+10+18+28) \\ A=60 \end{gathered}`

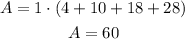
Thus, the approximate area under the curve between the given limits is 60 square units.