The diagram below represents the area approximated using rectangular elements,
The interval width when an interval [a,b] is divided into 'n' rectangles is given by,
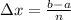
According to the given problem,
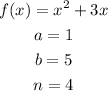
Then the width of each interval will be,
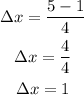
The left end-points of the approximating rectangles are,
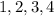
The value of the function at that left end-point gives the height of that rectangle. So the height of each rectangle will be,
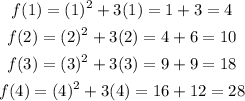
Then the approximate area (A) under the curve between the limits is given by the sum of the areas of all these 4 approximating rectangles,

Substitute the values and simplify,
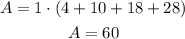
Thus, the approximate area under the curve between the given limits is 60 square units.