The Pythagorean theorem lets us relate the value of the sides of the triangles and its hypotenuse when we have a right triangle.
When you have the information about 2 of the three sides, you can use the relation:
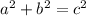
where a and b are sides of the triangle, and c is the hypotenuse.
Example:
You have a right triangle with sides 3 and 4. What is the value of the hypotenuse?
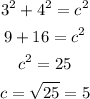
The trigonometry ratios can relate the values of the trigonometric functions of an angle and the value of the sides of the right triangle.
For example, we know that the sine of alpha (referring to the picture) is equal to the ratio between the adyacent side (the side that forms the angle, in this case "a") and the hypotenuse "c".
Then, when we know the angle, we can calculate a from c, or c from a using the expression:
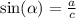
In the same way, the cosine of alpha is equal to the ratio of the opposite side (in this case "b") and the hypotenuse:
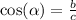
Using the definition of the tangent function, we can write:
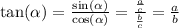
With this ratios we can relate any two pair of sides of the triangle.
The information we need is the value of one of the angles and one of the sides.