Question

I need help with homework D) y ≤ 1∕4x – 4

Answer 1

`c)y\ge(1)/(4)x-4`

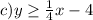
Step-by-step explanation

Step 1

let's find the equation of the line

a)slope

the slope of a line is given by:

`\begin{gathered} \text{slope}=\frac{chang\text{e in y}}{\text{change in x}}=(y_2-y_(1|))/(x_2-x_1) \\ \text{where} \\ P1(x_1,y_1) \\ \text{and } \\ \text{P2(x}_2,y_2) \\ \text{are 2 points from the line} \end{gathered}`

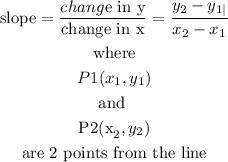
so

pick up 2 points from the line

let

P1=(0,-4)

P2=(4,-3)

now, replace in the equation to find the slope

`\begin{gathered} \text{slope}=(y_2-y_(1|))/(x_2-x_1) \\ \text{slope}=(-3-(-4))/(4-0)=(-3+4)/(4)=(1)/(4) \end{gathered}`

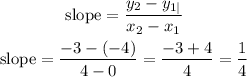
Step 2

b) the equation of the line, it can be found by using the poitn slope formula

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where m is the slope and } \\ P1(x_1,y_1) \end{gathered}`

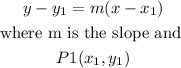
then, let

P1=(0,-4)

slope=1/4

replace and isolate y

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-4)=(1)/(4)(x-0) \\ y+4=(1)/(4)x \\ \text{subtract 4 in both sides} \\ y+4-4=(1)/(4)x-4 \\ y=(1)/(4)x-4 \end{gathered}`

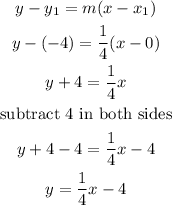
Step 3

finally, we need the shaded region, it means all the values over the line, in other words, the values greater than the function, so

`\begin{gathered} y=(1)/(4)x-4\Rightarrow shaded\text{ region }\Rightarrow y\ge(1)/(4)x-4 \\ \text{the line is continous so}\Rightarrow\ge \end{gathered}`

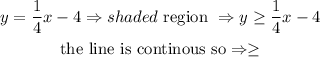
therfore, the answer is

`c)y\ge(1)/(4)x-4`

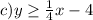
I hope this helps you