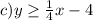
Step-by-step explanation
Step 1
let's find the equation of the line
a)slope
the slope of a line is given by:
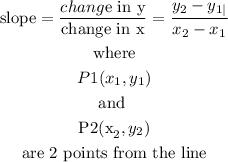
so
pick up 2 points from the line
let
P1=(0,-4)
P2=(4,-3)
now, replace in the equation to find the slope
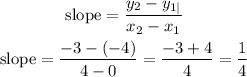
Step 2
b) the equation of the line, it can be found by using the poitn slope formula
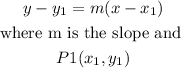
then, let
P1=(0,-4)
slope=1/4
replace and isolate y
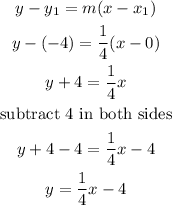
Step 3
finally, we need the shaded region, it means all the values over the line, in other words, the values greater than the function, so
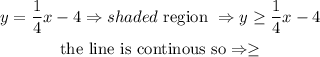
therfore, the answer is
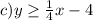
I hope this helps you