Question

<>. Question 5Engineers must consider the breadths of male heads when designing helmets. The company researchers havedetermined that the population of potential clientele have head breadths that are normally distributed with amean of 5.8-in and a standard deviation of 1.2-in. Due to financial constraints, the helmets will be designed tofit all men except those with head breadths that are in the smallest 1.5% or largest 1.5%.What is the minimum head breadth that will fit the clientele?min =What is the maximum head breadth that will fit the clientele?min =Enter your answer as a number accurate to 1 decimal place. Answers obtained using exact z-scores or Z-scoresrounded to 3 decimal places are accepted.Question Help: VideoSubmit Question

Answer 1

EXPLANATION

Let's see the facts:

Mean= 5.8 inches

Standard deviation = 1.2 inches

Smallest = 1.5% = 0.015

Largest = 1.5% = 0.015

First we need to compute te z-value in the smallest 1.5%

`P(0.015)=-2.17`

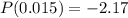
As we already know, the z-score is given by the following relationship:

`z=(x-\mu)/(\sigma)`

Isolating x:

`z\sigma=x-\mu`

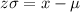
Adding +u to both sides:

`z\sigma+\mu=x`

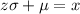
Switching sides:

`x=z\sigma+\mu`

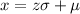
Replacing terms:

`x=-2.17\cdot1.2+5.8=3.196\text{ inches}`

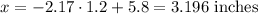
We can apply the same reasoning to the largest head breadths:

`P(0.985)=2.17`

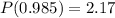
As the z-score is equal to 2.17 we can apply the same reasoning than the smallest in order to get the required measure:

`x=2.17\cdot1.2+5.8=8.404\text{ inches}`

In conclusion, the minimum head breadth is 3.2 inches and the maximum head breadth is 8.4 inches.