Question

A 7.80-g bullet moving at 690 m/s penetrates a tree trunk to a depth of 5.30 cm.(a) Use work and energy considerations to find the average frictional force that stops the bullet. (Enter the magnitude.)____ N(b) Assuming the frictional force is constant, determine how much time elapses between the moment the bullet enters the tree and the moment it stops moving._____ s

Answer 1

We are given that a 7.8g bullet is moving with an initial velocity of 690 m/s. It penetrates a trunk to a depth of 5.3 cm. To determine the value of the frictional force we will determine first the total energy that is carried by the bullet.

We use the formula for kinetic energy since this is the energy associated to velocity:

`K=(1)/(2)mv^2`

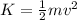
Now, we substitute the value for the initial velocity:

`K_0=(1)/(2)(0.0078kg)(690(m)/(s))^2`

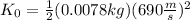
Solving the operations we get:

`K_0=1856.79J`

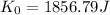
Since the bullet stops the final velocity is zero and therefore, the final kinetic energy is also zero:

`K_f=0`

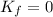
Now, this energy is lost due to the work done by the frictional force. The work done is given by:

`W=K_f-K_0`

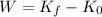
Also, the work done by a force is:

`W=F\cos\theta d`

Where:

`\begin{gathered} F=\text{ force} \\ \theta=\text{ angle between the force and the displacement} \\ d=\text{ displacement} \end{gathered}`

Since the kinetic force acts in opposite direction to the displacement this means that the angle is 180, therefore:

`W=F\cos180d=-Fd`

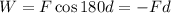
Now, we set both equations for work equal:

`-Fd=K_f-K_0`

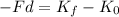
Now, we plug in the values of the kinetic energy:

`-Fd=0-1856.79J`

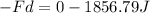
Now, we divide both sides by "-d":

`F=(-1856.79J)/(-d)`

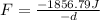
Now, we substitute the value of the displacement:

`F=(-1856.79J)/(-0.053m)=35033.77N`

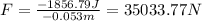
Therefore, the friction force is 35033.77 Newtons.

Part B. To determine the time that it takes the bullet to stop completely we need to determine first the acceleration of the bullet. We determine the acceleration using Newton's second law:

`F=ma`

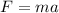
Where "F" is in this case is the friction force. Now, we divide both sides by "m":

`(F)/(m)=a`

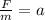
Now, we substitute the values:

`(35033.77N)/(0.0078kg)=a`

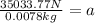
Solving the operations:

`4.5*10^6(m)/(s^2)=a`

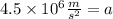
Now, we use the following equation of motion:

`v_f=v_0+at`

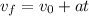
Now, we solve for "t". First, we subtract the initial velocity:

`v_f-v_0=at`

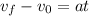
Now, we divide both sides by "a":

`(v_f-v_0)/(a)=t`

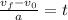
Now, we plug in the values:

`(0-690(m)/(s))/(-4.5*10^6(m)/(s^2))=t`

We use negative acceleration due to the fact that the bullet is deaccelerating:

Solving the operations:

`0.00015s=t`

Therefore, the time it takes the bullet to stop is 0.00015s