Question

Study the diagram of circle A, where BC is tangent to circle A at point C.Also, BC = 3, BA = 5, and AC is a radius.

Answer 1

A tangent to a circle is a straight line that touches the circle at only one point. This point is called the point of tangency.

One of the Circle Theorems states that the radius of a circle is perpendicular to the tangent line through its endpoint on the circle's circumference. This means that in the circle in the question, lines AC and BC are perpendicular.

Therefore, the triangle ABC is a right-angled triangle where AB is the hypotenuse.

The Pythagorean Theorem can be used to evaluate the measure of the radius. This theorem is stated to be

`hyp^2=opp^2+adj^2`

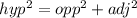
From the image, we have:

`\begin{gathered} hyp=AB=5 \\ opp=AC=r \\ adj=BC=3 \end{gathered}`

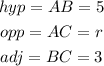
Substituting, we have:

`\begin{gathered} 5^2=r^2+3^2 \\ 25=r^2+9 \\ r^2=25-9 \\ r^2=16 \\ r=\sqrt[]{16} \\ r=4 \end{gathered}`

The FIRST OPTION is the correct option.