Question

Find the equation of the asymptote of f (x) = 3^(2x+1) + 3.

Answer 1

Asymptotes

An asymptote is a line that a curve approaches, as it heads towards infinity.

We need to find if the given function has a defined trend when x heads towards infinity or find the limit when x increases or decreases without limits

`\lim _{x\to-oo\text{ }}3^{\mleft\{2x+1\mright\}}+3`

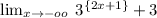
The exponent tends to zero when x tends to minus infinity, thus:

`\lim _{x\to-oo\text{ }}3^{\{2x+1\}}+3=0+3=3`

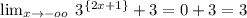
The line y=3 is a horizontal asymptote.

When x tens to plus infinity, the given function tends to infinity also, thus the limit:

`\lim _{x\to+oo\text{ }}3^{\{2x+1\}}+3=\infty`

Does not exist.

There is only one asymptote with the equation y=3