Question

Find the domain, vertical asymptotes, and horizontal asymptotes of the function.f(x)=x/x^2−9

Answer 1

Given the function

`f(x)=(x)/(x^2-9)`

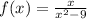
Notice that

`x^2-9=(x-3)(x+3)`

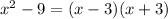
Therefore,

`\Rightarrow f(x)=(x)/((x-3)(x+3))`

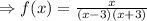
Notice that, if the denominator of f(x) is zero,

`\begin{gathered} (x-3)(x+3)=0 \\ \Rightarrow x=-3,3 \end{gathered}`

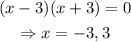
Therefore, the two vertical asymptotes are x=-3 and x=3.

The domain of the function includes all the real numbers except those excluded by the vertical asymptotes; thus, (the domain is shown below)

`\text{domain}=\mleft\lbrace x\in\R|x\\e-3,x\\e3\mright\rbrace=(-\infty,-3)\cup(-3,3)\cup(3,\infty)`

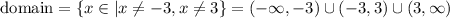
Finally, notice that the degree of the numerator is 1 while the degree of the denominator is 2. Since 2>1, the degree of the denominator is greater than that of the numerator. The horizontal asymptote is y=0.