Question

An assignment is worth 350 points. For each day the assignment is late, the professor deducts 10 points from the assignment grade. Write a linear function that represents the maximum number of points the assignment may receive at a given time, assuming it was turned in after it was due.

Answer 1

Given:

The total number of points is 350.

The points deduced for late by each day is 10.

The objective is to find the linear function that represents the maximum number of points the assignment may receive at a given time.

Consider the number of days as x, the received points as y.

Then, the equation can be represented as,

`y=350-10x`

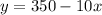
To obtain the limits, substitute y = 0 in the above equation,

`\begin{gathered} 0=350-10x \\ 10x=350 \\ x=(350)/(10) \\ x=35 \end{gathered}`

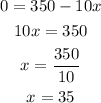
Thus, the value of x lies between,

`y=350-10x\text{ 0}\le x\le35`

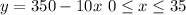
Now, assume the number of days after the due date as x = 5 days. Then the obtained points will be,

`\begin{gathered} y=350-10(5) \\ y=350-50 \\ y=300\text{ points} \end{gathered}`

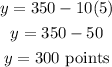
Now, assume the assignment was due by maximum number of 35 days. Then, the obtained points will be,

`\begin{gathered} y=350-10(35) \\ y=350-350 \\ y=0 \end{gathered}`

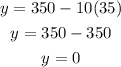
So, if the assignment was delay by 35 days, the obtained points will be zero.

Now, assume the number of days after the due date as x = 1 day. Then the obtained points will be,

`\begin{gathered} y=350-10(1) \\ y=350-10 \\ y=340 \end{gathered}`

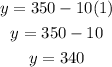
Thus maximum number of points that can be obtained by after it was due is 340 points.

Hence, the required linear function is y = 350-10x, with 0≤x≤35.