Question

A sheet of cardboard measuring 12 inches by 5 inches is curved tocreate a cylinder. It can be done in two ways.Which cylinder has larger volume?

Answer 1

The dimension of the cardboard is 12in by 5in

So when the cardboard is curved into a cylinder

there are two ways to do that

If diagram 'a' is folded into a cylinder

the circunference of the circular base form is 5 inches

then the radius is 0.8 in

since circuference = 2x pi x r

If diagram 'b' is folded into a cylinder

the circumference of the circular base is 12 inches

then the radius is 1.9 in

the volume

`\text{volume of a cylinder=}\pi* r^2* h`
`\begin{gathered} \text{for diagram 'a'} \\ \text{volume = 3.142}*0.8^2*12=24.1in^3 \end{gathered}`
`\begin{gathered} \text{for diagram 'b'} \\ \text{volume = 3.142 }*1.9^2*5=56.7in^3 \end{gathered}`

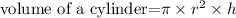
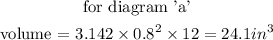
So diagram b gives the larger volume

Hence, when the cardboard in curved in such a way that the 12 inches side forms the base, the volume is larger than when the cardboard is curved such that the 5 inches side forms the base