Question

Determine which of the value(s), if any, must be excluded from the domain of the variable in the expression x/x^2-25x=0,x=-5,x=3,x=5

Answer 1

Given the expression below

`(x)/(x^2-25)`

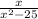
The expression above will have domains that will exclude the values of x for which the expression is undefined. The expression is undefined when the denominator is equal to zero

Therefore, it means that the values of x that must be excluded from the domain of the variable in the expression would be found as calculated below:

`\begin{gathered} (x)/(x^2-25) \\ \text{the denominator is} \\ x^2-25 \\ \text{the values of x for which the denominator is zero would be} \\ x^2-25=0 \end{gathered}`
`\begin{gathered} 25=5^2 \\ x^2-25=x^2-5^2=0 \\ u\sin g\text{ expansion of difference of two squares} \\ a^2-b^2=(a-b)(a+b) \end{gathered}`
`\begin{gathered} \text{Therefore,} \\ x^2-5^2=0,\text{ becomes} \\ (x-5)(x+5)=0 \\ x-5=0,or,x+5=0 \\ x=5,or,x=-5 \end{gathered}`

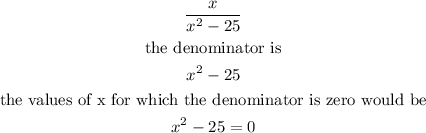
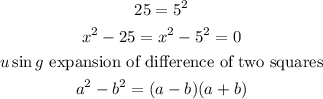
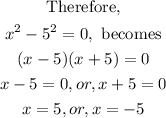
Hence, the values of x that must be excluded from the domain of the variable in the expression are x= 5 and x= -5