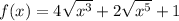Since we have the first derivative of function f, then, we can find f as follows:
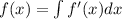
We can rewrite the given expression as follows

because
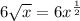
and

So, we need to compute
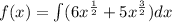
From the integration formula:
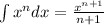
we get
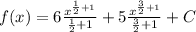
where C is the constant of integration. From this result, we have
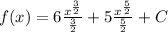
which gives
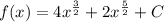
or equivalently,

Finally, we can find C by substituting the given information about f(x), that is, f(1)=7. It yields,
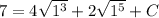
which gives
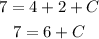
Then

Therefore, the answer is: