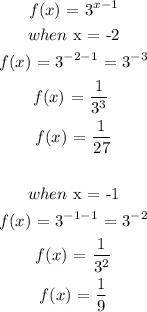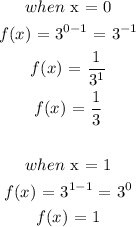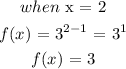Answer:
when x = -2, f(x) = 1/27
when x = -1, f(x) = 1/9
when x = 0, f(x) = 1/3
when x = 1, f(x) = 1
when x = 2, f(x) = 3
Step-by-step explanation:
Given:
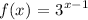
To find:
to get the y values for x = -2, -1, 0, 1, and 2
To determine the corresponding values of f(x), we will substitute each of the values into the given function