Let "x" represent the number of sheep and "y" represent the number of chickens.
If there are a total of 21 animals in the pen, we can express the number of animals there with the following expression
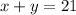
Each sheep has 4 legs, the number of legs per ship multiplied by the number of sheep indicates the total number of sheep legs there are: "4x"
Each chicken has two legs, multiply the number of legs per chicken by the number of chickens to determine the total number of chicken legs: "2y"
With the following expression, we can express the total number of legs in the pen as:
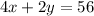
With these two expressions, we have determined a system of equations from which we can calculate the values of x and y.
The first step is to write the first equation for one of the variables, for example, for x:
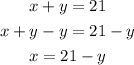
The second step is to replace the expression obtained for x in the second equation this way