Question

A deck of cards contains 10 black cards and 10 red cards. The first card drawn is not replaced before drawing the second card.What is the probability of selecting a red card followed by a red card? 141019519938

Answer 1

The probability of an event is expressed as

`P(event)=\frac{number\text{ of desirable outcome}}{number\text{ of possible outcome}}`

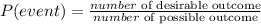
Given:

`\begin{gathered} number\text{ of black cards = 10} \\ number\text{ of red cards = 10} \\ Total\text{ number of cards = 20} \end{gathered}`

In this case, the number of possible outcomes is 20.

Given that the first card is drawn and not replaced before drawing the second card, the probability of selecting a red card followed by a red card is expressed as

`P(red\text{ and red\rparen=P\lparen first red\rparen}* P(second\text{ red without replacement\rparen}`

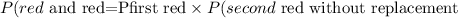
For the first red, we have

`\begin{gathered} P(first\text{ red\rparen=}\frac{number\text{ of red cards}}{number\text{ of cards\lparen number of possible outcomes\rparen}}=(10)/(20) \\ \Rightarrow P(first\text{ red\rparen=}(1)/(2) \end{gathered}`

For the second card, we have

`\begin{gathered} P(second\text{ red\rparen=}\frac{number\text{ of red cards left}}{number\text{ of cards left}}=(10-1)/(20-1) \\ =(9)/(19) \end{gathered}`

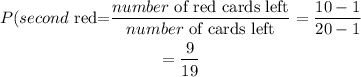
Thus,

`\begin{gathered} P(\text{ first red and second red\rparen=}(1)/(2)*(9)/(19) \\ \Rightarrow P(\text{ first red and second red\rparen=}(9)/(39) \end{gathered}`

Hence, the probability of selecting a red card followed by a red card is evaluated to be

`(9)/(38)`

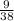
The fourth option is the correct answer.