We will have to make i feel calculations to get this.
Starting, we know that the cosine of the substraction between two angles can be calculated using the cos and sin values for each of thouse angles and the following equation:
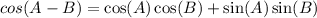
But we only know cos A, so we will have to figure the others.
Since they are acute angles, we can use a right triangle to get the other trigonometric calues for A and B.
Imagine a right triangle with one of the angles being A, its adjacent leg being 12 and the hypotenuse being 13:
This will make cos A be equal to 12/13, so this is a valid right triangle. Let's use Pythagora's Theorem to calculate the missing leg:
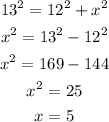
Now that we know it, we can calculate sin A by using the opposite leg and the hypotenuse:
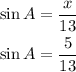
For B, we will do another right triangle and, since we know that tan B is 28/45, we will have an angle of B with opposite leg 28 and adjacent leg 45:
With Pythagora's Theorem we calculate the hypotenuse:
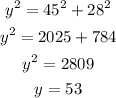
So, with all sides, we can calculate sin B and cos B:
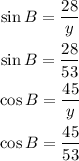
Now, we know all the parts needed:
