Step-by-step explanation
We have a total of 26 in the standard alphabet, 5 of them are vowel and the remaining 21 are consonants.
Also, we have 9 non-zero numbers.
The restrictions don't mention that we can't repeat letters or numbers, so we will assume we can repeat.
Since the first 2 spaces are consonants, we can pick each of them from 21 possibilities, so the combinations for that part are:

The next three are the non-zero numbers, so we can pick each from 9 possibilities:
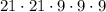
And the last is a vowel, so we can only pick from the 5 possibilities, so we have:
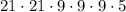
These are all the possibilities, so we just need to evaluate the product:
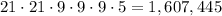
Answer
So, there are 1,607,445 possibilities.