Question

ASAP NEED HELP really bad please

Answer 1

1) See attachment.

2a) Initial Amount = 3600.
Growth/Decay factor = ³/₂.

2b) Growth function.

`\textsf{3)}\;\;\; f(x)=1*2^x`

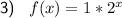
4) 69 lions.

Explanation:

General form of an exponential function

`\boxed{y=ab^x}`

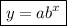
where:

• x is the independent variable.
• y is the dependent variable.
• a is the initial value (y-intercept).
• b is the base (growth/decay factor) in decimal form.

If b > 1 then it is an increasing function.

If 0 < b < 1 then it is a decreasing function.

Question 1

Given function:

`f(x)=\left((1)/(2)\right)^x`

Complete the table of ordered pairs by substituting the values of x into the given function:

`\begin{array}c\cline{1-2}x&y\\\cline{1-2}-3&8\\\cline{1-2}-2&4\\\cline{1-2}-1&2\\\cline{1-2}0&1\\\cline{1-2}1&0.5\\ \cline{1-2}\end{array}`

Plot the ordered pairs on the given coordinate plane (see attached graph) and draw a curve through them.

This exponential function has a horizonal asymptote at y = 0.

As the value of x approaches infinity, the function gets closer and closer to y = 0 (x-axis) but doesn't actually touch it.

Question 2

Given exponential function:

`f(x)=3600\left((3)/(2)\right)^x`

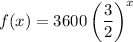
Part 2a

To find the initial amount "a" and growth/decay factor "b", simply compare the given function with the general exponential function.

Therefore:

• Initial Amount = 3600.
• Growth/Decay factor = ³/₂.

Part 2b

As b = ³/₂ and ³/₂ > 1, this is a growth function (increasing).

Question 3

"a" is the initial value (y-intercept) of an exponential function.

The y-intercept of a function is the y-value when x = 0.

Therefore, from inspection of the given table, the y-intercept of the given function is 1.

Therefore, a = 1.

"b" is the base (growth/decay factor) of an exponential function.

To find the base (growth/decay factor) of the given function, divide a value of y by its preceding value of y:

`\implies b=(4)/(2)=(2)/(1)=(1)/((1)/(2))=...=2`

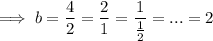
Therefore, b = 2.

So the exponential function for the given table is:

`f(x)=\boxed{1}*\boxed{2}\;^x`

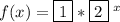
Question 4

If the population of lions started at 80, then the initial value "a" of the exponential function is 80.

If the population has been decreasing by 3.5% per year, then the population each year is 96.5% of the previous year since:

• 100% - 3.5% = 96.5%

Therefore, the base "b" of the exponential function is 0.965 (in decimal form).

Substitute the found values of a and b into the exponential function formula to create an exponential function for the given scenario:

`\boxed{f(t)=80(0.965)^t}`

where:

• f(t) is the number of lions.
• t is the time (in years).

To find how many lions will there be in four years, substitute t = 4 into the found exponential equation:

`\implies f(4)=80(0.965)^4=69.37440005`

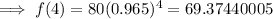
Therefore, there will be 69 lions in four years.