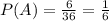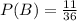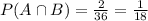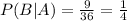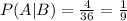To find the probability we need to count each one of the cases.
The event A is the sum of the dices are 7, since the dices are distinguishable between them we have that the event A is the set:
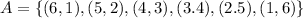
Now the event B is the set:
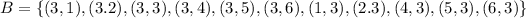
Now that we have our sets A and B we can calculate the other ones:
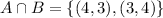
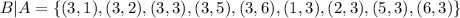
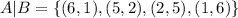
Now that we have all our sets we have to count how many cases each of them have and divided them by the total number os possible outcomes (36).
Then: