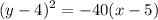Given, vertex: (5,4) focus (-5,4).
Since the y coordinates of the vertex and the focus are the same, the focus and the vertex are on the same horizontal line, y=4. So,the axis of symmetry is a horizontal line.
SInce vertex: (5,4) and focus (-5,4), we find that the focus is at the left of the vertex. So, the parabola opens leftwards.
So, the equation of parabola is,
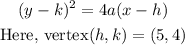
a=-5-(5)=-10 , since y coordinates are same.
Now, above equation becomes,
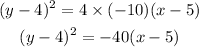
So, the equation of the parabola is,