Given the function:
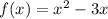
Let's solve for f(5).
To solve the function f when we have the indicated value f(5), substitute 5 for x in the function and solve.
Thus, we have:
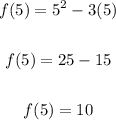
Let's solve for f(x) = 4.
To solve when f(x) = 4, substitute 4 for f(x) amd solve for the values of x.
Thus, we have:

Factorize the left side using the AC method:
Find a pair of numbers whose product is 4 and sum is -3.
We have:
-4 and 1
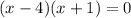
Set each factor to zero and solve for x:

Therefore, if f(x) = 4, then x = 4 and -1.
The grap represents a function because it passes the vertical line test.
The graph does not represent a one-to-one function.
ANSWER:
• f(5) = 10
,
• If f(x) = 4 then x = 4 and -1
,
• The graph represents a function.
,
• The graph does not represent a one-to-one function.