Question

Find the open interval where the function is increasing and decreasing. y=x^2+2x+3 (involves solving the derivative)

Answer 1

We have the next given function:

`y=x^2+2x+3`

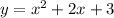
The equation corresponds to a parabola.

First, we need to derivate it:

`\begin{gathered} (d)/(dx)y=(d)/(dx)(x^2+2x+3) \\ Then \\ (d)/(dx)y=(d)/(dx)x^2+(d)/(dx)2x+(d)/(dx)3 \\ (d)/(dx)y=2x+2+0 \\ (d)/(dx)y=2x+2 \end{gathered}`

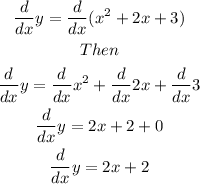
Now, we need to find when x=0.

`\begin{gathered} 2x+2=0 \\ Solve\text{ for x} \\ 2x=-2 \\ x=-(2)/(2) \\ x=-1 \end{gathered}`

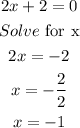
So, we can check the numbers using the number line:

Now, we need to check a number smaller than -1 and another number greater than -1.

Let us check 3.

Then:

`\begin{gathered} 2x+2 \\ 2(3)+2 \\ 6+2 \\ 8 \end{gathered}`

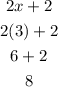
POSITIVE, when the x value is greater than -1, the function is positive (it is increasing).

Let us check -2:

`\begin{gathered} 2x+2 \\ 2(-2)+2 \\ -4+2 \\ -2 \end{gathered}`

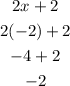
NEGATIVE, when the x value is smaller than -1, the function is decreasing.

Finally, we can write each interval.

The function is decreasing on interval (-∞,-1)

The function is increasing on interval (-1,∞)