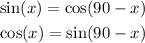Question

Consider the parent graphs of sine and cosine. a. How do the shapes of the graphs compare? b. What can you do to the graph of y = cos(x) to obtain the graph of y = sin(x)? c. Write an equation for the graph of y = sin(x) using a transformation of cosine. d. Write an equation for the graph of y = cos(x) using a transformation of sine. e. Based on your answers to parts (C) and (d), write an equation relating sine and cosine.

Answer 1

The graph of sine and cosine are

The shape are similar. However, there is a 90 shift difference

For instance, when x= 0, we get

`\begin{gathered} \sin (0)=0 \\ \text{and} \\ \cos (0)=1 \end{gathered}`

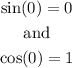
Now, when x=Pi/2 (90 degrees), we get

`\begin{gathered} \sin ((\pi)/(2))=1 \\ \text{and} \\ \cos ((\pi)/(2))=0 \end{gathered}`

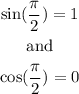
that is, the role has changed when x changes from 0 to 90 degrees. Then, the phase difference between them is 90 degrees (Pi/2)

b) What can you do to the graph of y = cos(x) to obtain the graph of y = sin(x)? We must translate cosine function 90 degrees (Pi/2) to the right, that is

`y=\sin (x)=\cos (90-x)`

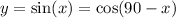
c) Write an equation for the graph of y = sin(x) using a transformation of cosine

From the last relationship,

`\sin (x)=\cos (90-x)`

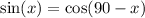
d) Write an equation for the graph of y = cos(x) using a transformation of sine.

In this case, we have the inverse process, that is

`\cos (x)=\sin (90-x)`

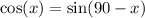
e). Based on your answers to parts (C) and (d), write an equation relating sine and cosine. ​

The equations are

`\begin{gathered} \sin (x)=\cos (90-x) \\ \cos (x)=\sin (90-x) \end{gathered}`