SOLUTION
The given ratio of adults to childeren is:
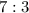
Let the total number of people be x then the number of adult and chlderen is:
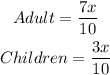
When 90 adult joins, the number of adult becomes:
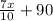
It is given that the number of adults would be 3 times the number of children.
It follows:
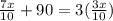
Solving for x gives:

Therefore the total number of people is 450.
It is given that 3/4 of the seat were occupied.
Let the total number of seats be y, it follows:
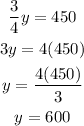
Therefore the total number of seats is 600