Question

There are 3 consecutive odd integers with a sum of –195. What is the least of these integers?

Answer 1

The 3 consecutive odd numbers are -67, -65 and -63 and the least of them is -67.

Step-by-step explanation:

Consecutive odd numbers means that the next number will be two more than the previous one.

Let the 1st number be y, the other 2 consecutive odd numbers will be y + 2 and y + 4.

We're also told that the sum of the 3 numbers is -195, so our equation can be written thus;

`y+(y+2)+(y+4)=-195`

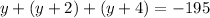
Let's collect like terms and solve for y;

`\begin{gathered} 3y+6=-195 \\ 3y=-195-6 \\ 3y=-201 \\ y=-(201)/(3) \\ \therefore y=-67 \end{gathered}`

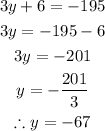
So our 1st number is -67.

Let's go ahead and find the other 2 numbers;

2nd number: y + 2 = -67 + 2 = -65

3rd number: y + 4 = -67 + 4 = -63

Therefore, the 3 consecutive odd numbers are -67, -65 and -63 and the least of them is -67.