Question

95) Which is the equation of a circle that has adiameter with endpoints (1, 3) and (-3, 1)?A. (x + 1)2 + (y - 2)2 = 10B. (x + 1)2 + (y - 2)2 = 20C. (x + 1)2 + (y - 2)2 = 5D. (x - 1)2 + (y - 2)2 = 5

Answer 1

Equation of a Circle

The equation of a circle with center at (h,k) and radius r is:

`(x-h)^2+(y-k)^2=r^2`

We know the endpoints of a diameter of a circle are (1,3) and (-3,1). The center of the circle is located at the midpoint of the segment.

Let's find the coordinates of the midpoint:

`x_m=(x_1+x_2)/(2)=(1-3)/(2)=(-2)/(2)=-1`

`y_m=(y_1+y_2)/(2)=(3+1)/(2)=(4)/(2)=2`

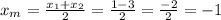
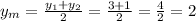
The center is located at (-1,2)

The radius is the distance from the center to any of the endpoints. Let's calculate that distance:

`r=\sqrt[]{(-1-1)^2+(2-3)^2}=\sqrt[]{4+1}=\sqrt[]{5}`

Thus, the equation of the circle is:

`\begin{gathered} (x+1)^2+(y-2)^2=(\sqrt[]{5})^2 \\ \text{Operating:} \\ (x+1)^2+(y-2)^2=5 \end{gathered}`

Choice C.