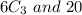Question

Can someone help me with these probability questions it’s only a two parter?

Answer 1

Given:

The number of players on the basketball = 14 players.

The number of juniors =6 players.

The number of seniors = 8 players.

Coach Banet decided to choose three players.

Required:

A. We need to find different orders of the top three finishers.

B. We need to find the probability that the top three finishers will all be seniors.

Step-by-step explanation:

A.

There is not important to choose in the order which players are the top three finishers.

Use combinations.

The number of students, n=14.

The number of the top three finishers, r =3.

`nC_r=14C_3`

`=(14!)/(3!(14-3)!)`

`=(14!)/(3!\cdot11!)`

`=364`

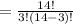
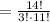
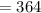
Answer:

`nC_r=(14!)/(3!\cdot11!)=364`

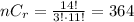
B.

The number of seniors = 8 players.

The number of top-finishers =3.

`8C_3=(8!)/(3!(8-3)!)=(8!)/(3!\cdot5!)=56`

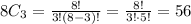
There are 56 different orders of top finishers that include all seniors.

`The\text{ possible outcome=}14C_3`
`T\text{he favorable outcome =}8C_3`

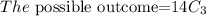
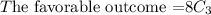
The probability that the top three finishers will all be seniors.

`P=(8C_3)/(14C_3)`
`Use\text{ }14C_3=364,\text{ and }8C_3=56.`

`P=(56)/(364)`

`P=0.1538`

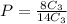
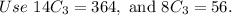
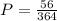
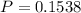
Multiply by 100 to get a percentage.

`P\text{ \%}=0.1538*100`

`P\text{ \%}=15.38\text{ \%}`

`P\text{ \%}=15.4\text{ \%}`

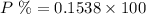
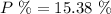
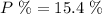
Answer:

There are 56 different orders of top finishers that include all seniors.

The probability that the top three finishers will all be seniors is 15.4 %

1)

B)

The number of juniors = 6 players.

The number of players in the group =3.

There is not important to choose in the order which players are selecting.

Use combinations.

`6C_3=(6!)/(3!(6-3)!)=(6!)/(3!\cdot3!)=20`

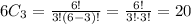
Answer:

Two terms represent the number of players that are all juniors.

`6C_3\text{ }and\text{ }20`