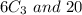Given:
The number of players on the basketball = 14 players.
The number of juniors =6 players.
The number of seniors = 8 players.
Coach Banet decided to choose three players.
Required:
A. We need to find different orders of the top three finishers.
B. We need to find the probability that the top three finishers will all be seniors.
Step-by-step explanation:
A.
There is not important to choose in the order which players are the top three finishers.
Use combinations.
The number of students, n=14.
The number of the top three finishers, r =3.
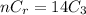
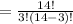
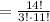
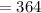
Answer:
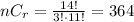
B.
The number of seniors = 8 players.
The number of top-finishers =3.
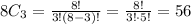
There are 56 different orders of top finishers that include all seniors.
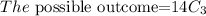
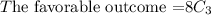
The probability that the top three finishers will all be seniors.
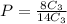
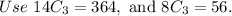
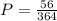
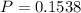
Multiply by 100 to get a percentage.
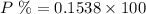
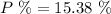
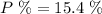
Answer:
There are 56 different orders of top finishers that include all seniors.
The probability that the top three finishers will all be seniors is 15.4 %
1)
B)
The number of juniors = 6 players.
The number of players in the group =3.
There is not important to choose in the order which players are selecting.
Use combinations.
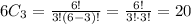
Answer:
Two terms represent the number of players that are all juniors.