The form of the direct variation is
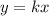
Where k is the constant of variation
Since the given figure is a parabola that represents a quadratic equation, then
The equation should be
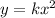
Let us use the points on the graph to check if all values of k will be equal
If they are equal, then it is a direct variation,
if they are not equal, then it is not a direct variation
Let us use points (2, 2), (4, 8), and (-3, 4.5)
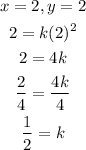
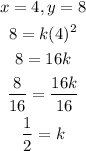
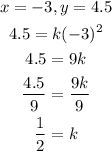
Since the values of k are equal, then it is a direct variation
Yes, it is a direct variation