The distance between two points (x1, y1) and (x2, y2) is:
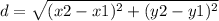
Using the Pythagorean theorem for the right triangle with hypotenuse "h" and sides "a" and "b", we have:
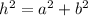
To find "h", "a", and "b", we have to find the distance between the points.
Distance between A(8, 1) and B(0, 4):
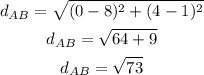
Distance between A(8, 1) and C(-8, -3):
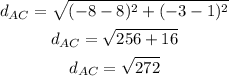
Distance between B(0, 4) and C(-8, -3):
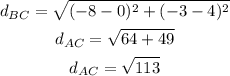
Now, let's compare the sides using the Pythagorean theorem. Remember h must be the greatest side.

Since 272 is not equal to 186, the triangle is not a right triangle.
Answer: NO.