Question

Is the triangle with the vertices A(8,1), B(0,4), and C(-8,-3) a right triangle?Is the triangle a right triangle?YesNo

Answer 1

The distance between two points (x1, y1) and (x2, y2) is:

`d=√((x2-x1)^2+(y2-y1)^2)`

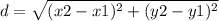
Using the Pythagorean theorem for the right triangle with hypotenuse "h" and sides "a" and "b", we have:

`h^2=a^2+b^2`

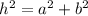
To find "h", "a", and "b", we have to find the distance between the points.

Distance between A(8, 1) and B(0, 4):

`\begin{gathered} d_(AB)=√((0-8)^2+(4-1)^2) \\ d_(AB)=√(64+9) \\ d_(AB)=√(73) \end{gathered}`

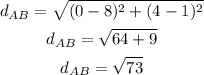
Distance between A(8, 1) and C(-8, -3):

`\begin{gathered} d_(AC)=√((-8-8)^2+(-3-1)^2) \\ d_(AC)=√(256+16) \\ d_(AC)=√(272) \end{gathered}`

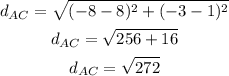
Distance between B(0, 4) and C(-8, -3):

`\begin{gathered} d_(BC)=√((-8-0)^2+(-3-4)^2) \\ d_(AC)=√(64+49) \\ d_(AC)=√(113) \end{gathered}`

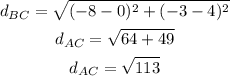
Now, let's compare the sides using the Pythagorean theorem. Remember h must be the greatest side.

`\begin{gathered} √(272)^2=√(73)^2+√(113)^2 \\ 272=73+113 \\ 272=186 \\ WRONG \end{gathered}`

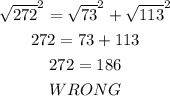
Since 272 is not equal to 186, the triangle is not a right triangle.

Answer: NO.