Let X be a random variable that is distributed as a normal distribution with mean 40 and standard deviation = 4. We want to calculate following probability
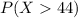
To do so, we will use a standard normal distribution, which is a normal distribution with mean 0 and standard deviation 1. So, we will transform the variable X in a variable Z that has a standard normal distribution. To do so we subtract the mean of X to X and then divide it by its standard deviation. That is, define
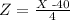
So, this variable Z has a standard normal distribution with mean 0 and standard deviation of 1.
So, we want to translate this probability
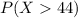
to a probabilty using the variable Z. So we if we start with this inequality
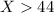
if we subtract 40 on both sides, we get
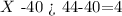
Now, if we divide both sides by 4, we get
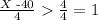
So the initial inequality is the same as the following

So, we have the following equivalence
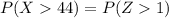
Using the properties of probability, we have that
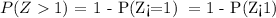
Using a table for the left side area of a standard normal distribution, we have that
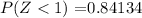
So we have
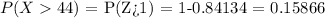
So, the probability of selecting a score greater than 44 is 0.15866