Question

I must get my math grade up and I need help. Please help me, I am unfamiliar with the material and need explaining/Thanks so much!

Answer 1

Step-by-step explanation

`\mathrm{The\: area\: between\: curves\: is\: the\: area\: between\: a\: curve}\: f\mleft(x\mright)\: \mathrm{and\: a\: curve}\: g\mleft(x\mright)\: \mathrm{on\: an\: interval}\: \mleft[a,\: b\mright]\: \mathrm{given\: by}`

We can see that the needed area is defined between x=0 and x=6, and is below the curve y= sin^-1 (x/6)

First, computing the area below the curve y= sin^-1 (x/6):

Applying integration by parts:

`\int \: uv^(\prime)=uv-\int \: u^(\prime)v`
`u=\arcsin \mleft((x)/(6)\mright)`
`v^(\prime)=1`
`(d)/(dx)\mleft(\arcsin \mleft((x)/(6)\mright)\mright)`

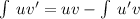
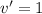
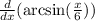
Apply the chain rule:

`(df(u))/(dx)=(df)/(du)\cdot(du)/(dx)`
`f=\arcsin \mleft(u\mright),\: \: u=(x)/(6)`
`=(d)/(du)\mleft(\arcsin \mleft(u\mright)\mright)(d)/(dx)\mleft((x)/(6)\mright)`
`(d)/(du)\mleft(\arcsin \mleft(u\mright)\mright)`

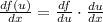
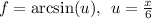
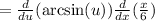
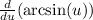
Apply the common derivative:

`(d)/(du)(\arcsin (u))=\frac{1}{\sqrt[]{1-u^2}}`
`=(1)/(√(1-u^2))`
`=(1)/(√(1-u^2))(d)/(dx)\mleft((x)/(6)\mright)`
`\mathrm{Substitute\: back}\: u=(x)/(6)`
`=\frac{1}{\sqrt{1-\left((x)/(6)\right)^2}}(d)/(dx)\mleft((x)/(6)\mright)`

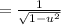
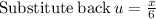
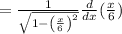
Taking the constant out and applying the common derivative:

`=\frac{1}{\sqrt{1-\left((x)/(6)\right)^2}}(d)/(dx)\mleft((x)/(6)\mright)`