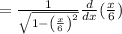Step-by-step explanation
![\mathrm{The\: area\: between\: curves\: is\: the\: area\: between\: a\: curve}\: f\mleft(x\mright)\: \mathrm{and\: a\: curve}\: g\mleft(x\mright)\: \mathrm{on\: an\: interval}\: \mleft[a,\: b\mright]\: \mathrm{given\: by}](https://img.qammunity.org/2023/formulas/mathematics/college/44hsq0fb72ygs2larcfrszhe1o2qloqm9e.png)
We can see that the needed area is defined between x=0 and x=6, and is below the curve y= sin^-1 (x/6)
First, computing the area below the curve y= sin^-1 (x/6):
Applying integration by parts:
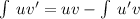
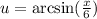
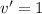
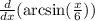
Apply the chain rule:
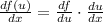
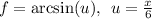
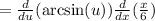
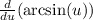
Apply the common derivative:
![(d)/(du)(\arcsin (u))=\frac{1}{\sqrt[]{1-u^2}}](https://img.qammunity.org/2023/formulas/mathematics/college/96azn1y858filoez3gwguniox7vyz2ntdl.png)
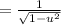
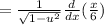
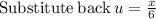
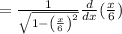
Taking the constant out and applying the common derivative: