Question

You have learned how to divide polynomials in three different ways: by factoring, by long division, and by synthetic division. Explain in words and with mathematical representations how you would divide this polynomial in each of the three ways.

Answer 1

Step-by-step explanation:

Given:

`\frac{6x^3+24x^2-2x-8}{x\text{ + 4}}`

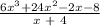
To find:

To divide polynomials using factoring, long division, and synthetic division

NB: In the absence of example on factoring method, we will only be considering long division and synthetic division

Using long division:

For long division, the divisor will be outside(x + 4) while the expression to be divided (6x³ + 24x² - 2x - 8) will be inside the dividing section.

Divide 6x³ by x. The result is 6x². Write the result at the quotient. Then multiply 6x² by (x + 4). This gives 6x³ + 24x². Subtract 6x³ + 24x² from the original expression. 6x³ + 24x² cancels out. We will be left with -2x - 8.

Divided -2x by x. This gives -2. Write this at the quotient. Multiply -2 by (x + 4). The result is -2x - 8. Subtract -2x -8 from (-2x - 8). The result is zero. This means there is no remainder.

The result of the division is 6x²- 2

Using synthetic division:

For this division, the coefficients are used. The coefficients of the polynomial 6x³ + 24x² - 2x - 8 are 6, 24, -2, -8

The divisor used in the division is the value of x when x + 4 is equated to zero

x + 4 = 0

x = -4

We bring down the first coefficient beneath the line.

1) Multiply that coefficient by the divisor (-4). This gives -24. Write -24 in the 2nd row. Add this result to the coefficient at the top (24). The result is 0

2) Multiply -4 by 0. The result will be written in the 2nd row under the next coefficient (-2). Add 0 to -2. 3) The result -2 is multiplied by -4. We get 8. This is added to the next coefficient (8). The sum gives 0

When the last number of a synthetic division is zero, it means there is no remainder. It was factorized completely.

The final result of the division from the synthetic division: