To complete the table, we want to choose any value on the given intervals and test its sign on each columns, (t - 2) and (t - 1). If both have + signs, the las column will also have + sign. If both have - sign, the last column will have + sign. If one has + sign and the other has - sign, the last column will have - sign.
The first internal is "less than 1 hour".
One easi pick here is t = 0:
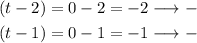
Since both are negative, we have:

So, the first row is:
less than 1 hour - - +
The second is not an interval it is "1 hour", so:
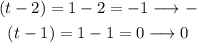
Since any number multiplied by 0 is also 0, the result on the third column will also be 0:
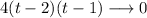
So, the second row is:
1 hour - 0 0
The third interval is "between 1 and 2 hours", so we can pick 1.5, for example. We have:
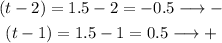
Since one is - and the other is +, the third column will be negative:
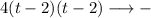
So, the third row is:
between 1 and 2 hours - + -
In the fourth, we have a value of 2 hours, so:
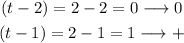
Since one of them is 0, the third column will also be 0, so:
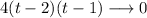
So, the fourth row is:
2 hours 0 + 0
The last interval is "more than 2 hours", so we can pick 3, for example:

Since both are +, the third column will also be +:

So, the fifth row is:
more than 2 hours + + +
So, we have:
interval of time (t-2) (t-1) 4(t-2)(t-1)
less than 1 hour - - +
1 hour - 0 0
between 1 and 2 hours - + -
2 hours 0 + 0
more than 2 hours + + +