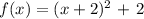
Here, we are given a quadratic equation graph and we are tasked with getting the equation of the quadratic equation from the graph
The first thing we need to note here is the shape of the parabola.
This in the sense that if the parabola opens up or faces down
On the graph we can see that the parabola faces the positive x-direction
Generally, the equation of a quadratic graph is usually in the form below;
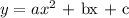
So by identifying the values of a,b and c, we can get the complete equation of the graph
The above form is called the standard form while the form we have in the options is referred to as the vertex form
The vertex form can be written as;

Now, looking at the graph, we can see that the graph crosses the y-axis at the point y = 6
At this point, the value of x is 0
The vertex (h,k) represents the center point of the parabola
In the case of this question, the point is (-2,2)
so h =-2 and k is 2
What is left is to get a
we can obtain this from the value of y = 6 and x = 0
Thus;
6 = a(0-(-2))^2 + 2
6 = a(2)^2 + 2
6 = 4a + 2
4a = 6-2
4a = 4
a = 4/4 =1
So the equation in the vertex form is f(x) = (x + 2)^2 + 2