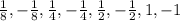Question

Use the Rational Root Theorem to find and list all the possible roots of the polynomials:

Answer 1

The Rational Root Theorem states that if all the coefficients (the numbers multiplying the powers of x) are integers and the constant term (the number not multiplied by any power of x) is not zero then all the roots are equal to a factor of the constant term divided by a factor of the leading coefficient (the number multiplying the greatest power of x).

So let's write these factors. First the factors of the constant term 1. 1 only have two integer factors: 1 and -1.

The leading coefficient is 8 and its integer factors are: 8, -8, 4, -4, 2, -2, 1 and -1. This means that the possible roots for this polynomial are:

`(1)/(8),-(1)/(8),(1)/(4),-(1)/(4),(1)/(2),-(1)/(2),1,-1`

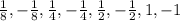
We should evaluate the polynomial in all of these values and those which result in zero are its roots. If we do this you'll see that the following values result in zero:

`\begin{gathered} f(-(1)/(4))=8\cdot(-(1)/(4))^3+2\cdot(-(1)/(4))^2+4\cdot(-(1)/(4))+1 \\ f(-(1)/(4))=-(1)/(8)+(1)/(8)-1+1 \\ f(-(1)/(4))=0 \end{gathered}`

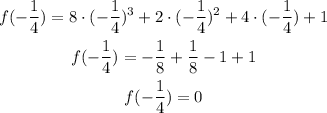
And this is the only value for which the result of replacing the x with it results in 0. Then the root is -1/4.

The problem asked to list all the possible roots. Those are in the following list that is the solution to the problem:

`(1)/(8),-(1)/(8),(1)/(4),-(1)/(4),(1)/(2),-(1)/(2),1,-1`