Final answer:
The expression (7x³y²)^²⁷ results in 7²⁷x⁸¹y⁵⁴ by applying the rule
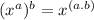 . Converting to radical form would typically involve the variables, but since there are no fractional exponents, the numbers usually remain in exponential form.
. Converting to radical form would typically involve the variables, but since there are no fractional exponents, the numbers usually remain in exponential form.
Step-by-step explanation:
The expression (7x3y2)27 in radical form is obtained by applying the property (ax)b = ax. b. In this case, each factor in the parentheses is raised to the power of 27, which gives us 727x81y54. This follows the same logic as the rule (xa)b = xa. b which states that when raising an exponential expression to a power, you multiply the exponents.
When converting to radical form, 727 remains as it is because we usually keep numbers in their exponential form unless the power is a fraction. Therefore, the radical form of the given expression would typically be written with the variables under the radical sign, if necessary.